A
termodinâmica nos fornece todos os balanços de massa e energia de um
sistema e podemos, através da equação da energia livre de Gibbs,
determinar se um processo é espontâneo ou não. Entretanto, pelas equações
da termodinâmica, não é possível prever em quanto tempo o processo
ocorrerá, mesmo sendo espontâneo. O exemplo clássico é o do diamante. A
energia livre de Gibbs da reação de conversão do diamante para o carvão é
de aproximadamente -2500kJ mol-1 e, portanto, o processo é
espontâneo. Porém, a cinética desta reação é muito lenta e podemos
afirmar, ao menos na escala de vida de um ser humano, que os diamantes são
eternos.
![]()
A cinética é a parte da química
que estuda as velocidades das reações químicas e os fatores que as
influenciam. A velocidade de uma reação pode depender de variáveis sob nosso
controle como pressão, temperatura ou pela presença de um catalisador e,
assim, pode ser otimizada pela escolha apropriada de condições.
Catalisadores são componentes que não alteram as constantes de equilíbrio das reações químicas, mas diminuem a energia de ativação da conversão de reagentes em produtos e alteram sua velocidade. São amplamente utilizados na indústria para acelerar reações que produzem substâncias de interesse econômico mas que seriam muito lentas sem eles. Constituem, assim, fator de desenvolvimento econômico.
A primeira etapa na análise
da cinética de reações é estabelecer a estequiometria da reação e
identificar quaisquer reações laterais. Os dados básicos da cinética química
são as concentrações dos reagentes e produtos em diferentes intervalos de
tempo após uma reação ter iniciado. As velocidades da maioria das reações
químicas são sensíveis à temperatura e, em experimentos convencionais de cinética,
a mistura reacional é mantida sob temperatura constante durante o curso da reação.
Assim, a reação genérica:
![]()
Possui as seguintes velocidades de alteração (formação ou consumo) das espécies:
![]() (1)
(1)
Ou, de maneira genérica:
![]() (2)
(2)
Onde vJ
As velocidades das reações
podem ser proporcionais à concentração dos reagentes elevadas a uma potência.
Por exemplo, a velocidade de uma reação genérica pode ser dada por:
![]() (3)
(3)
A equação (3) também é
chamada de lei de velocidade de uma reação e deve ser determinada
experimentalmente, não podendo ser inferida pela equação geral da reação. O
coeficiente k
é chamado de constante de velocidade da reação; é independente da concentração
de qualquer espécie, mas depende da temperatura do sistema.
Na equação (3) a concentração de cada espécie está elevada a um coeficiente; estes não representam os coeficientes estequiométricos da reação química, e exprimem a ordem da reação com respeito a cada espécie, bem como definem sua ordem global. Assim, lei de velocidade expressa pela equação (3) é de ordem a com relação à espécie A, b com relação à espécie B. A ordem global da reação é dada por a+b. A ordem da reação pode ser fracionária.
Quando a ordem global da reação é igual a zero, ou seja, v=k, a velocidade da reação não depende da concentração de qualquer dos reagentes. Quando v=k[A] a reação depende da concentração do reagente A. Como esta concentração está elevada à primeira potência diz-se que a reação é de ordem zero. Existem reações com as mais variadas ordens, incluindo fracionárias. Entretanto, seu tratamento matemático é consideravelmente complexo. Portanto, neste artigo, manter-nos-emos à cinética de ordem um.
A ordem de uma reação pode ser determinada pelo método de isolamento, onde as concentrações de todas as espécies exceto uma é mantida em grande excesso. Assim, aproxima-se que a concentração das espécies em excesso mantém-se constante durante todo o processo. Deste modo, se a lei de velocidade de uma reação for dada por v=k[A][B] e [B] for mantida constante, pode-se reescrever a lei de velocidade como:
![]()
![]() (4)
(4)
Na equação (4), k’ representa a constante de velocidade aparente, e a lei de velocidade é tida como de pseudo-primeira ordem.
Outro método comumente utilizado, normalmente em conjunto com o método de isolamento, é o das velocidades iniciais, onde a velocidade é medida no começo de uma reação para várias concentrações iniciais de reagentes. Assim, se a lei de velocidade de uma reação é dada por v = k’[A]a, então a velocidade inicial v0 será dada pelos valores iniciais de concentração de A, e pode-se escrever v = k’[A]0a. Tomando logaritmos obtém-se:
![]() (5)
(5)
As constantes de velocidade da maioria das reações aumentam conforme a temperatura é elevada. Svante August Arrhenius determinou que a dependência da constante de velocidade das reações com a temperatura é dada pela equação:
![]() (6)
(6)
Onde A é uma constante, Ea é a energia de ativação da reação, R é a constante dos gases e T a temperatura absoluta. O termo pré-exponencial “A” e a energia de ativação “Ea” de uma reação podem ser obtidos determinado-se constantes de velocidade em várias temperaturas. A equação (6) pode ser modificada para:
![]() (7)
(7)
Assim, o gráfico de lnk por 1/T fornecerá uma reta com coeficiente angular igual a –Ea/RT e intercepto igual a lnA.
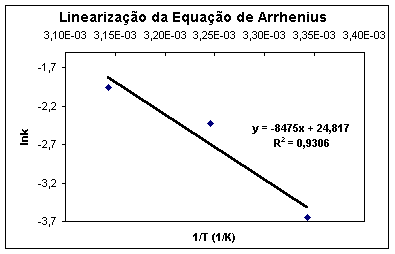
Figura 1 - Exemplo de linearização da função de Arrhenius
O método experimental adotado para acompanhar as mudanças de concentração de uma ou mais espécies depende de suas características e da velocidade das alterações. Reações muito rápidas requerem técnicas especiais de monitoramento, como análise em tempo real, em fluxo, por inibição da reação ou por fotólise. Reações relativamente lentas podem ser acompanhadas, entre outras técnicas, por medição espectrofotométrica da absorção de luz por uma espécie química presente no sistema reacional. A técnica é especialmente apropriada quando a substância possui absorção característica numa região de fácil acesso do espectro UV/VIS. Também pode-se acompanhar a conversão de compostos quirais (que desviam o plano da luz polarizada) pela inversão ou anulamento de seus centros assimétricos utilizando um polarímetro.
A.Krell